My Ancestors

This article contains a lot of maths. I’m bound to have made a mistake or been ambiguous somewhere and so I’d welcome any feedback, questions, corrections or indeed suggestions for other things you’d like me to look at or consider. Just add a comment. Thank you.

The grandparent problem

Some of the mathematics of family history is mind boggling. Almost all of us have 2 parents, 4 grandparents, 8 great grandparents etc, but if you continue this simple series you run into a brick wall. Go back thirty generations – perhaps 750 years – and we each have over one billion 28 x great grandparents. And that’s a problem, because it is more than the entire global population at that time.

What’s going on here? The only way this apparent conundrum can be resolved is if I accept that amongst my 1 billion 28 x great grandparents there must be a lot of duplicates. How could this happen?

Let’s assume for the moment that a pair of my great grandparents were first cousins. This would mean they shared one pair of grandparents. This in turn would mean that I would have 30 3 x great grandparents rather than 32. And this would then mean that 25 generations further back I would be looking for around 70 million (or 7%) fewer 28 x great grandparents.

The only connection like this that I’m currently aware of in my own tree is that I believe that the two grandmothers of my 3 x great grandmother Eliza Ann STOURTON (nee LANGTON) (1807-1863) were in fact cousins. If I’ve done my maths correctly then this means that I in fact have 510 7 x great grandparents rather than 512. And, as a consequence, 21 generations further back from this I would be looking for around 4 million (or 0.4%) fewer 28 x great grandparents.

This doesn’t look like it’s making enough of a difference. I suspect that all of us have many, many more links and connections waiting to be discovered within our trees. A lot of those links might well stem from times before the Industrial Revolution when many of our ancestors lived in villages and seldom travelled or settled far from home. First and second cousin marriages would have been much more frequent in those times. As a thought experiment, if half my 4,096 10 x great grandparents (who might have lived around 300 years ago) married their first cousins then I think this would mean I’d have 12,298 12 x great grandparents rather than 16,384. And 16 generation further back this would mean I would be looking for around 270 million (or 27% fewer 28 x great grandparents). This is certainly making a more meaningful difference to the numbers.

We’re all much more closely connected than we think

This sort of thinking and analysis can – and has been – extended to think about (and use DNA to analyse) how inter-connected we all are. As an aside, politicians and warring factions the world over might care to take heed of this … but almost certainly won’t. A 2020 Scientific American article provides a good summary and has some links to other papers. Essentially the paper is saying that if we all did our family trees then:

• Around 2,000 to 3,000 years ago every one of us would have a pair of individuals that appeared on all of our trees; and then, even more remarkably;
  
• Around 4,000 to 7,000 years ago every one of us would have exactly the same individuals listed across the tops of our trees. Yes, there would have been other individuals living at that time, but they have no living descendants today.

And as the article – which can be found here https://www.scientificamerican.com/article/humans-are-all-more-closely-related-than-we-commonly-think/ – concludes (in words that are musical to the ears of any family historian) we are all connected to royalty: we’re each very special and very generic, both at the same time.

How many fourth cousins do I have?

Some time ago I concluded that it might be possible to trace with reasonable certainty all of my 32 3 x great grandparents. They were all born into Georgian Great Britain and almost all lived into the early part Victorian era, a time when registration of births, marriages and deaths became routine, and an era from which decennial census records survive. Would it then be possible to trace each descendant of each of the 16 couples? Each couple’s 3 x great grandchildren would be my first, second, third or fourth cousins (… or of course me and my siblings). How many of these might I expect to find?

Clearly this crucially depends on the number of children each couple has (not counting those who don’t survive to adulthood and those who don’t marry).

Another assumption I’m going to make is that spouses of cousins count as cousins. You could choose not to count them but it makes the maths just a bit more complex.

Let’s start with a simple example, just going back to my grandparents and asking how many first cousins I’d have if each couple had three children. We end up with the following picture showing 44 individuals and 24 first cousins…

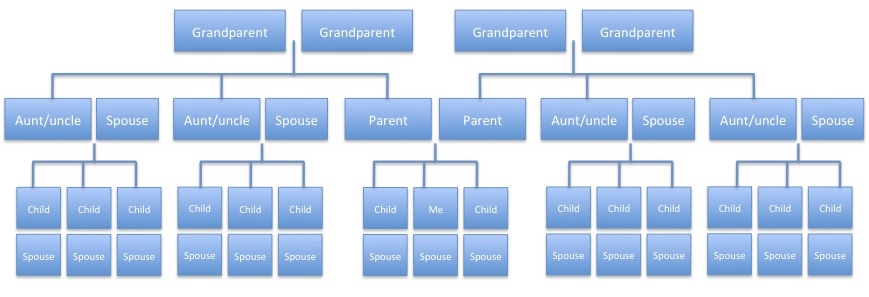
It’s possible to rework this assuming each couple had n children. In this case we find we have:

• 4n² + 2n + 2 individuals; and
• 4n x (n – 1) first cousins

You can check both of these when n = 3

And then we can sit in a darkened room and work out how this would work if we went back three more generations. We find we have:

• 32n⁵ + 16n⁴ + 8n³ +4n² + 2n + 2 individuals; and
• 32n⁴ x (n – 1) first, second, third and fourth cousins

So if each of my ancestors had three children who survived to adulthood, married and had three children who did the same, I can expect to be writing about 9,332 individuals and I would need to find 5,184 first, second, third and fourth cousins (24 first, 120 second, 720 third and 4,320 fourth ones if you’re curious!).

Fecundicity

I’ve always quite liked that word! The ability to produce an abundance of offspring. I was always told that my Nana CLARK was descended from a number of very large families, whereas Grandad CLARK’s family was much smaller. The maths above is providing me with a helpful way to measure this.

Firstly, I look at the tree the other way. Rather than look ‘up’ the tree I can focus in on each pair of 3 x great grandparents and look ‘down’ and ask how many descendants and cousins should stem from each pair. It turns out the answer is:

• 2n⁵ + 2n⁴ + 2n³ +2n² + 2n + 2 individuals; and
• 2n⁴ x (n – 1) 3 x great grandchildren (including spouses, but excluding me and my siblings) (i.e. my first, second, third and fourth cousins)

So with n = 3 I expect to find 728 descendants (including my 3 x great grandparents in this number) and 324 first, second, third and fourth cousins.

For comparison, if n = 2 the numbers become 126 descendants and just 32 first, second, third and fourth cousins, but if n = 4 they shoot up to become 2,730 descendants and 1,536 first, second, third and fourth cousins.

And then I can see how many I’m actually managing to trace in different branches of my own tree. Having put in an equivalent amount of effort – obviously a subjective judgment – and looking at the male ancestors of my Grandad and my Nana, I currently have in my tree:

• William Taylor CLARK (1795-1869) and Ann OSBOURN (c.1787-1877):
  294 descendants and 82 3 x great grandchildren
  
• Joseph BEVERS (1789-?) and Elizabeth KING (1791-?):
  651 descendants and 195 3 x great grandchildren

(The descendant figures exclude 4 and 5 x great grandchildren and their spouses. The 3 x great grandchildren figures include spouses but exclude me and my siblings.)

So for the CLARK’s the descendant number implies n = 2.4 and the 3 x great grandchildren number implies n = 2.3. Whereas for the BEVERS the descendant number implies n = 2.9 and the 3 x great grandchildren number implies n = 2.7

Whilst their giving reasonably consistent answers, I’m not surprised the 3 x great grandchildren number leads to a lower answer – later generations are harder to trace reliably due to the need to protect confidentiality for living individuals.

We could use the descendants’ number to attach a ‘Fecundicty Index’ to each branch of the tree. So, based on my research to date, my latest scores are 2.3 for the CLARKs and 2.9 for the BEVERS.

Conclusions

This has been a bit of a ramble through some mathematics. I’m sure there are many other opportunities to apply maths to help the family historian and I’m happy to add to this page as they come to me or based on any feedback or questions.